Golden Ratio

Regé-Jean Page ⁴

SYMBOLISM

ARCHITECTURE

GLOBES, PILLARS & COLUMNS

INDEX OF PAPERS

Download a 1.1MB PDF essay on the Golden Rato by clicking here.

View a 520k PowerPoint presentation on the Golden Rato by clicking here.

The golden section

Although not naming it the Golden Ratio, around 300 BCE Euclid of Alexandria defined the proportion: "A straight line is said to have been cut into extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser." The precise value of the Golden Ratio is an irrational number, phi (1.61803399...), and, like the irrational number pi (3.14159265...) or e (2.71828183...), was considered by the Pythagoreans to be so horrific that its knowledge should be kept secret.

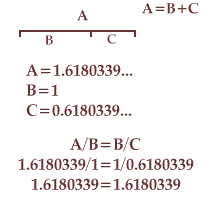The Golden Section, or Golden Ratio, divides a line at a point such that the smaller part relates to the greater as the greater relates to the whole: the ratio of the lengths of the two sides is equal to the ratio of the longer side to the sum of the two sides.

a/b

= b/a+b
= a+b/a+2b
= a+2b/2a+3b
= 2a+3b/3a+5b &c.

Fra Luca Paciola (1445-1517) published Divina Proportione in Venice in 1509. The first of the three volume text contained a detailed summary of the properties of the Golden Ratio. Up until Paciola’s time, the Golden Ratio had been known as "extreme and mean ratio" or "proportion having a mean and two extremes" and the concept appears to have only been known to mathematicians.

The theological and philosophical implications in the name Divine Proportion, and Leonardo da Vinci’s drawings of polyhedra for the book, brought the ratio to the attention of a new audience of artists and intellectuals. Scientists have observed that patterns in nature—ranging from fish scales to spiral galaxies—exhibit a tendency to the Golden Ratio, but the actual knowledge or use of the Golden Ratio by early architects and artists remains a controversial claim.

It was first termed the Golden Section by German mathamatician, Martin Ohm in a footnote in the 1835 second edition of Die Reine Elementar-Mathematik: "One also customerily calls this division of an arbitrary line in two such parts the golden section [Goldene Schnitt]." In mathematics the common symbol for the Golden Ratio is the Greek letter tau from the Greek word for "the cut" or "the section". Early in the twentieth century an American mathematician gave the ratio the name of Φ [phi], the first Greek letter in the name of the Greek sculptor, Phidias (c. 490 BC-c. 430 BCE). This is the more common term today.

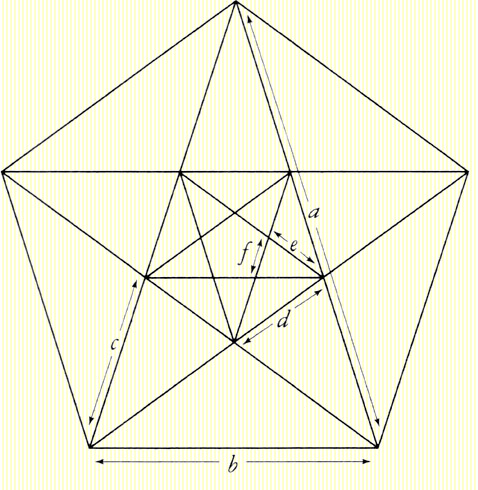
The Pythagorean fascination with the number 5 (the union of the first female number, 2, with the first male number, 3) and their admiration for the five-pointed star lead to their interest in the Golden Ratio.

Mathematicians label the geometric figure of a five-pointed star the pentagram, although occultists and symbolists will generally only style the never-ending knot as a pentagram. Of especial interest to freemasons, or students of esoteric philosophy, the geometric proportions of the pentagram are also those of the Golden Section, aurio sectio: Golden Mean.

"At any rate all his [Pythagoras'] school in serious letters to each other began straightway with 'Health to you,' as a greeting most suitable for both body and soul, encompassing all human goods. Indeed the Pentagram, the triple intersecting triangle which they use as a symbol of their sect, they called 'Health.'" ¹

"The striking property of all these figures is that if you look at line segments in order of decreasing length (the ones marked a, b, c, d, e, f in the figure), you can prove using elementary geometry that every segment is smaller than its predecessor by a factor that is precisely equal to the Golden Ratio, Φ [phi]." ²

Johannes Keppler (1571-1630) wrote : "Geometry has two great treasures; one is the Therorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel."

The Pythagorean theorem, a² + b² = c², while not neccessarily considered a "truth", was known as long ago as the Old Babylonian period (ca. 1600 BCE)

Golden rectangle

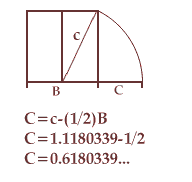If a square is added to the long side of a golden rectangle, a larger golden rectangle is formed. This ratio forms the foundation of the Fibonacci series of numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144..., where each number is formed by adding the previous two numbers.

The appearance of the golden ratio or fibonacci sequences in nature—the rotation of branches on flower stems, the rows of scales on a pineapple, the florets in sunflowers—is not a constant law of nature but a prevalent tendency.

Spira Mirabilis (Wonderful spiral)

Jacques Bernoulli (1654-1705) researched the logarithmic curve which features self-similarity: as its size increases, its shape remains the same. Also termed the equiangular spiral, the shells of some shellfish (although, contrary to popular belief, not the chambered nautilus), the horns of rams, and also sunflowers, hurricanes and giant spiral galaxies all have a tendency to this proportion. This spiral can be drawn by drawing curves inside a Golden Rectangle.

Fibonacci Numbers

The Fibonacci sequence was so called by the French mathematician, Edouard Lucas (1842-1891). It relates to the Golden Ratio because as the sequence progresses the rato of two successive Fibonacci numbers approaches the irregular Golden Ratio. This was discovered in 1611 by the German astronomer Johannes Keppler (1571-1630) and later proven, in a fashion, by the Scottish mathemetician Robert Simpson (1687-1768).

In a Fibonacci series, each number is the sum of the previous two numbers. Except for the number 1, any two adjacent numbers in the series, when seen as a ratio, are very close to the Golden Mean: 89/144= 0.61805555556; when seen as fractions, they make it easy to remember how to create or identify the golden section: 2/3, 5/8, 8/13, etc.
The Fibonacci series is formed by adding the latest two numbers to get the next one, starting from 0 and 1:

0		1
0	+	1	=	1
0		1		1
		1	+	1	=	2
0		1		1		2
				1	+	2	=	3
0		1		1		2		3

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, &c.³

Lucian of Samosata (c. 120 - 180 CE), Loeb edition. vol VI: Pro Lapsu... = In defence of a slip of the tongue in the middle of a greeting; Lucian, with an English Translation by A. M. Harmon. Volume 3, Loeb classical library. London : Heinemann, 1921. Cf.: "At any rate all the Pythagoreans in writing to one another (when their tone is serious, that is) started with wishing Health, which they took to be the prime need of soul and body alike, and to include all human blessings. The Pentagram, that interlaced triple triangle which served them as a sort of password, they called by the name Health." The Works of Lucian of Samosata tr. by H. W. Fowler and F. G. Fowler. Oxford: The Clarendon Press [1905]

Mario Livio (1945-), The golden ratio : the story of phi, the world's most astonishing number. New York, NY: Broadway Books, c2002. viii, 294 p. : ill. ; 24 cm. ISBN : 0767908155. p. 35. image page 34

Also see: goldennumber.net/
mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
mathworld.wolfram.com/FibonacciNumber.html
plus.maths.org.uk/issue3/fibonacci/index.html
ulcar.uml.edu/~iag/CS/Fibonacci.html
mathworld.wolfram.com/GoldenRatio.html

4. Harley Street facial cosmetic surgeon, Dr Julian De Silva, announced on 2023/01/27 that actor, Regé-Jean Page's face conforms 93.65 per cent to the golden ratio, equating this with handsomeness. Cited: firstpost.com [accessed 2023/01/28] Image: The Late Show With Stephen Colbert

© 1871-2024 Grand Lodge of British Columbia and Yukon A.F. & A.M. Updated: 2023/01/28
freemasonry.bcy.ca/symbolism/golden_ratio/index.html